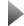Glaciologists have adopted a range of strategies to deal with this complexity. One common approach is to model the re- sponse of a small sample of glaciers, and then extrapolate the results to wider regions. Two basic types of models have been employed. First, static models compute how snow and ice melt rates will change under different climatic scenarios, but do not consider changes in glacier geometry (e.g. Radic and Hock, 2006). Second, dynamic models allow glacier dimen- sions and geometry to evolve through time, and can therefore include feedbacks between melt rates and glacier characteris- tics (e.g. Oerlemans et al., 1998; Schneeberger et al., 2003). While the second approach yields more robust results, dy- namic models must be tailored to individual glaciers and are very time-consuming to implement. Consequently, dynamic

Glacier volume change forecasts Normalized volume variation

120% 100% 80% 60% 40%

20% 0%

Temperature increase

Celsius degree per year 0.01

0.01* 0.02 0.02* 0.04 0.04*

Average 1980 2000 2020 2040 2060 2080 2100 Source: Oerlemans et al., Climate Dynamics, 1998

Figure 3: Scaled glacier volume changes for a range of climate scenarios. Labels are in degrees C yr–1 crease in precipitation per degree warming. The left-hand panel (<VSC

14 , and + indicates a 10% in- >) shows the average of all model results, and the right-hand panel (<V>SC) shows results weighted by glacier volume. (From Oerlemans et al., 1998: Climate Dynamics 14, 267–274)

* Includes a 10% precipitation increase per degree warming

models have been run for very few of the world’s glaciers and most predictions are based on static models with a tendency to overestimate mass loss (e.g. ACIA, 2005). Undoubtedly, there is great need for more glacial research, monitoring and inventories (Braithwaite, 2009; Shi et al., 2009).

Oerlemans et al. (1998) conducted modelling experiments for a sample of 12 glaciers and ice caps, to determine volume changes under a range of temperature and precipitation forcings (Fig. 3). The range of glacier response is very wide, so a key issue is finding ways to upscale the results of modelling this tiny sample of glaciers to large regions. Figure 2 shows the re- sults of two alternative weighting procedures. Although the absolute values of volume change differ, the results imply

Normalized volume variation 120%

100% 80% 60% 40%

20% 0%

Weighted average by glacier volume

1980 2000 2020 2040 2060 2080 2100